여러 개의 순서 인덱스 방식을 살펴볼 것이다. 각각의 기술은 DB 응용 프로그램에 맞게 사용하면 된다.
각각의 방식들은 다음과 같은요소에 기초해서 평가된다.
- 접근 유형(Access Type) : 효율적으로 지원되는 접근 유형.
접근 유형은특정 속성의 값을 가진 레코드나특정 범위에 들어가는 속성의 값을 가진 레코드를 찾는 것을 포함한다. - 접근 시간(Access Time) : 특정 데이터 항목이나 항목의 집합을 찾는데 걸리는 시간
- 삽입 시간(Insertion Time) : 새로운 데이터 항목을 삽입하는데 걸리는 시간. 여기에는 새로운 데이터 항목을 삽입하기 위한 정확한 위치를 찾는데 걸리는 시간과 인덱스 구조를 갱신하는데 걸리는 시간이 포함된다.
- 삭제 시간(Deletion Time) : 데이터 항목을 삭제하는데 걸리는 시간. 여기에는 데이터 항목을 삭제하기 위한 정확한 위치를 찾는데 걸리는 시간과 인덱스 구조를 갱신하는데 걸리는 시간이 포함된다.
- 공간 부담(Space Overhead) : 인덱스 구조가 차지하는 부가적인 공간.
파일 안에 있는 record에 대해 빠른 속도로 임의 접근(random access)을 하기 위해 인덱스 구조를 사용할 수 있다.
각 인덱스 구조는 특정한 검색 키와 관련있다. 책이나 도서관 목록과 같은 인덱스처럼 순서 인덱스(ordered indices)는 검색 키의 값을 정렬된 순서로 저장하고 검색 키와 검색 키를 포함한 레코드를 이어준다.
인덱스 파일의 record는 특정 속성에 의해 정렬된 순서로 저장될 수 있다.하나의 파일은 서로 다른 검색 키에 따라 여러 인덱스를 가질 수 있다.
■ 원하는 record를 포함한 파일의 레코드들이 연속적으로 정렬되어 있는 경우클러스터링 인덱스는 해당 파일을 연속적인 순서로 정의한 속성을 검색 키로 사용하는 인덱스다. 여기서 클러스터링 인덱스는 기본 인덱스(primary index)라고도 불린다.
ex) 이름 속성으로 정렬되어 있는 경우 ⇒ 클러스터링 인덱스는 이름 속성을 검색키로 사용한 인덱스가 된다.
비클러스터링 인덱스는 파일의 연속적인 순서와 다른 순서로 구성되는 검색 키의 인덱스이다.
앞으로 소개잘 2.1~2.3절의 모든 파일은 어떤 검색 키에 의해 연속적인 순서로 정렬되어 있다고 가정한다.
검색 키에 대해 기본 인덱스(클러스터링 인덱스)를 가지는 파일을 인덱스 순차 파일(index sequential file)이라 한다. 이는 DB 시스템에서 가장 오래된 인덱스 구조 중 하나다.
전체 파일의 연속적인 처리와 각 레코드에 대해 random access를 필요로 하는 응용 프로그램을 위해 이러한 인덱스를 설계한다.
- instructor 레코드의 순차 파일. 아래 예시에서 record는 검색 키로 사용된 교수 ID를 기준으로 정렬되어서 저장된다.

1. 밀집과 희소 인덱스 (Dense and Sparse Indices)
인덱스 레코드(또는 인덱스 엔트리)는 검색 key값과 포인터로 구성되어 있다.
이때, 포인터는 1개 이상의 레코드를 가리킨다. 그리고 포인터는 디스크 블록의 식별자와 블록 안에서 레코드를 구별하기 위한 디스크 블록 내부의 오프셋으로 구성되어 있다.
우리가 사용할 수 있는 순서 인덱스는 2가지 유형이 있다.
- 밀집 인덱스 (Dense Index)
밀집 인덱스에서인덱스 레코드는 파일에 있는모든 검색 키 값 마다나타난다.
1) 밀집 클러스터링 인덱스
밀집 클러스터링 인덱스에서 인덱스 레코드는 검색 key값과 해당 검색 key값의 첫 번째 데이터 레코드에 대한 포인터를 갖고 있다. 똑같은 검색 key값을 가진 나머지 레코드들은 첫 번째 데이터 레코드 이후부터 연속적으로 저장된다.
이는 인덱스가 클러스터링 인덱스여서 동일한 검색 key로 정렬되기 때문이다.
2) 밀집 비클러스터링 인덱스
똑같은 검색 key를 가진 모든 레코드에 대한 포인터 목록을 저장해야 한다.
- 희소 인덱스 (Sparse Index)
희소 인덱스에서인덱스 레코드는 검색 key값에 대해 일부만 나타난다.
희소 인덱스는 relation이 검색 key로 정렬되어 저장될 때, 즉 인덱스가 클러스터링 인덱스인 경우에만 사용할 수 있다.
밀집 인덱스처럼 각각의 인덱스 레코드는 검색 key값과 해당 검색 key값의 첫 번째 데이터 레코드에 대한 포인터를 갖고 있다.
레코드를 위치시키고 싶다면 찾고자 하는 검색 key값보다 작거나 같은 것 중 가장 큰 검색 key값을 가지는 인덱스 엔트리를 찾아야 한다.
ex) 찾고자 하는 검색 key값 = 8 / 8보다 작은 key값이 5라고 하면 5 다음에 위치하면 된다.
원하는 레코드를 찾고 싶다면, 인덱스 레코드가 가리키는 레코드를 시작으로 파일에서 원하는 레코드를 찾을 때 까지 포인터를 따라간다.
ex) 찾고자 하는 레코드의 검색 key값 = 5 / 5가 가리키는 첫 번째 레코드에서부터 원하는 레코드를 찾을 때 까지 포인터를 따라가야 한다.
그림 14.2와 14.3은 instructor 파일에 대한 밀집 인덱스와 희소 인덱스를 보여준다.

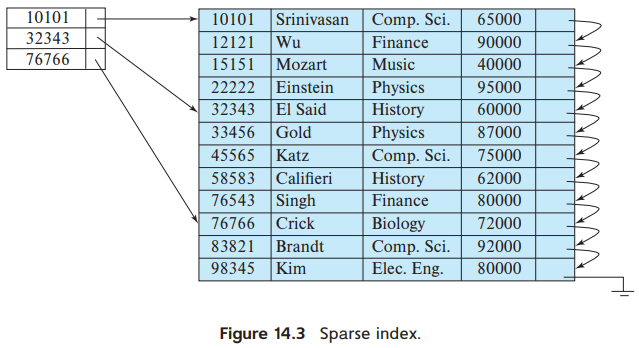
ex) ID = 22222 인 instructor의 레코드를 찾는다고 하자.
- 밀집 인덱스를 사용하면... 원하는 ID값을 가진 인덱스 레코드를 찾아서 그 레코드가 가리키는 포인터를 따라가면 된다.
- 희소 인덱스를 사용하면...
1) ID가 22222인 인덱스 레코드가 없기 때문에 22222 앞에 있는 10101 포인터를 따라간다.
2) 따라가고 나면 원하는 레코드를 찾을 때 까지 연속적인 순서로 instructor 파일을 읽는다.
사전을 생각해보자. 각 페이지의 헤더는 알파벳 순서로 각 페이지의 첫 번째 단어 목록이다. (a, b, c, d...)
사전 인덱스의 각 페이지의 제일 상단에 있는 단어는 해당 페이지에 대한 희소 인덱스를 제공한다. 그 단어를 기준으로 내가 원하는 단어가 해당 페이지에 있는지 그 페이지 앞/뒤에 있는지를 가늠할 수 있다.
그림 14.4는 검색 키가 primary key가 아닌 dept_name인 instructor 파일에 대한 밀집 클러스터링 인덱스를 보여준다.
이 경우에는 instructor 파일이 ID 대신에 검색 key인 dept_name을 가지고 정렬된다. 그렇지 않으면 dept_name은 비클러스터링 인덱스가 된다 .

ex) 찾고자 하는 레코드의 dept_name이 History라고 하면
위 그림의 밀집 인덱스를 이용하면 가장 앞에 있는 History 레코드를 가리킨 포인터를 통해 해당 레코드로 이동한다.
그렇게 다른 dept_name을 가진 레코드를 만날 때 까지 계속해서 포인터를 따라간다.
- 비교
- 밀집 인덱스 : 레코드의 위치를 찾아내는 속도가 빠르다
- 희소 인덱스 : 공간을 적게 차지해서 삽입/삭제에 대한 유지 부담이 더 적다.
시스템 설계자는 접근 시간과 공간 차지 사이의 trade-off를 고려해야 한다.
이에 대한 절충안은 1개의 블록당 1개의 인덱스 엔트리를 가지는 희소 인덱스를 가지는 것이다.
이렇게 정한 이유는 DB 요구를 처리하는데 드는 대부분의 비용은 disk에서 main memory로 블록을 가져오는데 걸리는 시간이기 때문이다. 일단 블록을 한 번 갖고 오면 해당 블록 전체를 scan하는데 시간이 많이 들지 않는다.
블록을 가리키는 희소 인덱스를 사용하면 찾고자 하는 레코드를 포함한 블록을 위치시킬 수 있다.
만약 이 레코드에 대한 오버플로 블록(13.3.2)이 없다면 인덱스의 크기를 최대한 작게 유지하면서 블록 접근을 최소화해야 한다.
앞의 기술들을 일반화하기 위해서 하나의 검색 key값에 대한 record가 여러 블록을 차지하는 경우에 대해서도 따져봐야 한다.
이러한 상황을 다루기 위해 구조를 변경하는 것은 어렵지 않다.
2. 다계층 인덱스(Multilevel Indices)
그냥 밀집 인덱스를 사용하는 경우
ex) 1,000,000개의 튜플을 가진 relation에 밀집 인덱스를 구축한다고 하자.
하나의 블록의 크기를 4KB라 하고 인덱스 레코드 (인덱스 엔트리)는 거기에 100개 들어갈 수 있다고 하자. ⇒ 인덱스는 10,000개의 블록을 차지한다.
ex) 100,000,000개의 튜플을 가진 relation에 밀집 인덱스를 구축한다고 하자 ⇒ 인덱스는 1,000,000개의 블록을 차지한다.
이러한 대용량의 인덱스는 디스크 상에 연속적인 파일로 저장된다.
- 인덱스가 메인 메모리에 저장될 만큼 크기가 작다면 ⇒ 인덱스 레코드를 찾는데 걸리는 시간은 당연히 짧다.
- 인덱스가 메인 메모리에 저장할 수 없을 만큼 크기가 크다면 ⇒ 인덱스를 디스크에 저장해야 하고 ⇒ 그러면 당연히 인덱스 레코드를 찾는데 걸리는 시간은 길어진다.
인덱스 파일 내에 엔트리의 위치를 정하기 위해 이진 검색을 사용하는 경우 ⇒ 비용이 많이 든다.
만약에 인덱스가 b개의 블록을 차지한다면 이진 검색은 [log_2(b)] 만큼 블록을 읽어야 한다.
읽어야할 블록이 인접하게 위치하지 않는다면 각 블록을 읽는 작업은 random하게 I/O 연산을 해야 한다.
ex) 10,000개의 블록으로 구성된 인덱스 ⇒ 14개의 블록 읽기가 필요 ⇒ 블록 1개를 읽을 때 10밀리초가 걸린다고 하면 140밀리초가 걸린다. 즉, 1초에 7개의 인덱스를 검색할 수 있다.
여기에 오버플로 블록이 존재한다면 실제 비용은 더 높아진다.
인덱스 파일 내에 엔트리의 위치를 정하기 위해 순차 검색을 사용하는 경우 ⇒ 비용이 더 많이 들어갈 수 있음
이진 검색, 순차 검색 둘 다 인덱스 파일의 크기가 크다면 비용이 더욱 많이 발생한다.
이런 문제를 해결하기 위해서 인덱스를 순차 파일처럼 취급해서 아래 그림과 같이 내부 인덱스(inner index)라고 불리는 기존의 기본 인덱스에 대한 sparse 외부 인덱스를 구성한다.
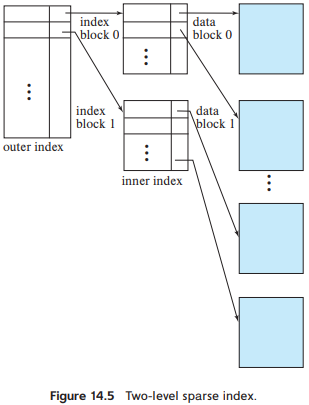
인덱스 레코드는 외부 인덱스를 희소(sparse)하게 분포시키며 항상 정렬된 순서로 존재한다.레코드의 위치를 찾고 싶다면...
1) 먼저 외부 인덱스에서 이진 검색을 이용해 원하는 레코드보다 작거나 같은 검색 key값 중에서 가장 큰 값을 가진 레코드를 찾을 수 있다.
2) 이때 레코드 포인터는 내부 인덱스 블록을 가리킨다.
3) 내부 인덱스의 블록을 스캔해서 원하는 레코드 보다 작거나 같은 검색 key값 중에서 가장 큰 값을 가지는 레코드를 찾는다.
4) 해당 레코드에 있는 포인터는 원하는 레코드를 포함한 파일의 블록을 가리킨다.
5) 같은 방식으로 파일의 블록을 스캔해서 원하는 레코드를 찾으면 된다.
앞선 예시를 상기하면
ex) `1,000,000개의 튜플을 가진 relation`에 밀집 인덱스를 구축한다고 하자.
하나의 블록의 크기를 4KB라 하고 인덱스 레코드 (인덱스 엔트리)는 거기에 100개 들어갈 수 있다고 하자. ⇒ 인덱스는 `10,000개의 블록`을 저장하면 된다.
즉, 내부 인덱스 엔트리 10,000개를 가지고 1,000,000개의 튜플을 가리킬 수 있다.내부 인덱스의 인덱스 엔트리 10,000개는 100개의 블록으로 표현할 수 있다.
즉, 외부 인덱스의 인덱스 엔트리 100개를 가지고 내부 인덱스 엔트리 10,000개를 표현할 수 있다.
그러면, 외부 인덱스의 인덱스 엔트리 100개는 1개의 블록으로 저장할 수 있다. 그래서, 원하는 데이터 레코드를 찾을 때 오직 하나의 인덱스 블록만 읽으면 된다.
그리고 외부 인덱스의 인덱스 엔트리의 개수는 100개이기 때문에 log_2(100) = 6.6xx => 7번의 읽기 작업이 필요.
즉, 메인 메모리에서 외부 인덱스가 저장된 블록을 하나 읽으면 70밀리초가 필요하다. 따라서, 1초에 14개의 인덱스를 검색할 수 있다.
파일이 너무 크다면 외부 인덱스의 크기도 커져서 메인 메모리에 전부 저장할 수 없다.
ex) `100,000,000개의 튜플을 가진 relation`에 밀집 인덱스를 구축 ⇒ 내부 인덱스는 `1,000,000개의 블록` ⇒ 외부 인덱스는 `10,000개의 블록` 즉, 40MB를 차지한다. 이렇게 많은 용량을 필요로 한다면 또 다른 단계의 인덱스를 생성해내면 된다. 이처럼 2개 이상의 단계를 가지는 인덱스를 다계층 인덱스라고 한다. 다계층 인덱스로 레코드를 찾으면 상당히 적은 입출력 연산을 수행할 수 있다. 또한 인덱스의 각각의 단계는 물리적 저장 장치와 대응할 수 있다.
다계층 인덱스는 메모리 인덱스에서 사용되는 이진 트리와 같은 트리 구조와 매우 밀접한 관련이 있는데 이에 대해서는 14.3에서 자세히 살펴볼 것이다.
3. 인덱스 갱신 (삽입 및 삭제)
모든 인덱스는 어떤 레코드가 파일에 삽입되거나 파일로부터 삭제될 때 마다 갱신되어야 한다.
파일 안에 있는 레코드가 갱신된 경우에도 갱신(update)에 영향을 받은 검색 키를 소유한 인덱스 역시 갱신되어야 한다.
ex) 교수의 소속 학과 변경 ⇒ instructor 릴레이션의 dept_name 속성에 대한 인덱스가 갱신되어야 한다.
인덱스의 갱신은 결국 이전 레코드의 삭제이후에 새로운 레코드 값의 삽입으로 이뤄진다.
따라서, 인덱스에 대한 삽입과 삭제에 대해서만 고려하면 되고 갱신에 대해서는 고려하지 않아도 된다.
여기서는 한 단계로 되어 있는 인덱스를 갱신하기 위한 알고리즘을 설명한다.
삽입 (insertion)
1) 삽입되는 record의 검색 key값을 이용해서 탐색을 수행한다.
2) 이후의 과정은 밀집 인덱스 vs 희소 인덱스에 따라 다른 과정을 수행한다.
- 밀집 인덱스
1) 검색 key값이 인덱스에 없다면 적당한 위치에 검색 key값을 가진 인덱스 엔트리를 삽입
2) 검색 key값이 인덱스에 이미 존재한다면 아래의 과정을 수행한다. 1) 만약에 기존에 있는 인덱스 엔트리가 똑같은 검색 key값을 가지는 모든 레코드를 가리키는 포인터를 저장하고 있다면 시스템은 인덱스 에느리에 삽입하려고 하는 레코드에 대한 포인터를 추가한다. 2) 그렇지 않다면 인덱스 엔트리는 검색 key값을 가지는 첫 번째 레코드에 대한 포인터만 저장하고 있다. 그러면 시스템은 똑같은 검색 key값을 가지는 다른 레코드 뒤에 삽입된 레코드를 놓는다.- 희소 인덱스
인덱스는각 블록에 대한 엔트리를 저장한다고 가정하자.
시스템이 새로운 블록을 생성한다면 새로운 블록에 나타나는 (검색 key 순으로) 첫 번째 검색 key값을 인덱스에 삽입한다.
반면, 새로운 레코드가 그 블록안에 있는 가장 작은 검색 key값이라면 시스템은 해당 블록을 가리키고 있는 인덱스 엔트리를 새로운 레코드의 검색 key값으로 갱신한다.
새로운 레코드가 그 블록안에 있는 가장 작은 검색 key값이 아니라면 블록에 있는 가장 작은 key값이 바뀌지 않으니까 시스템은 인덱스를 바꾸지 않는다.
삭제 (Deletion)
1) 먼저 삭제될 레코드를 찾는다.
2) 이후의 과정은 밀집 인덱스 vs 희소 인덱스에 따라 다른 과정을 수행한다.
- 밀집 인덱스
1) 삭제된 인덱스가 특정한 검색 key값을 가지는 유일한 레코드였다면 시스템은 인덱스와 대응되는 인덱스 엔트리를 삭제한다.
2) 유일하지 않다면 아래의 과정을 수행한다. 1) 인덱스 엔트리가 똑같은 검색 key값을 가지는 모든 레코드를 가리키는 포인터를 저장한다면 시스템은 인덱스 엔트리로 부터 삭제된 레코드에 대한 포인터를 삭제한다. 2) 인덱스 엔트리가 검색 key값을 가지는 첫 번째 레코드에 대한 포인터만 저장하고 있을 때 삭제된 레코드가 첫 번째 레코드였다면 시스템은 이전에 레코드를 가리키던 인덱스 엔트리가 다음 레코드를 가리키도록 갱신한다.- 희소 인덱스
1) 만약 인덱스가 삭제된 레코드의 검색 key값을 가진 인덱스 엔트리를 포함하지 않았다면 인덱스에 대해서 수행할 동작이 없다.
2) 삭제된 레코드의 검색 key값을 가진 인덱스 엔트리를 포함한다면 아래의 과정을 수행한다. 1) 삭제된 레코드가 검색 key값을 가진 유일한 레코드였다면 시스템은 대응되는 인덱스 레코드를 다음 검색 key값을 위한 인덱스 레코드로 교체한다. 다음 검색 key값이 이미 인덱스 엔트리에 있다면 해당 엔트리는 삭제된다. 2) 유일하지 않다면 검색 key값을 위한 인덱스 엔트리는 똑같은 검색 key값을 가지는 다음 레코드를 가리키도록 갱신된다.
다계층 인덱스를 위한 삽입과 삭제는 위에 설명했던 구조를 간단하게 확장하면 된다.
가장 낮은 단계에서 삭제 또는 삽입을 실행하고 단계를 하나씩 올라갈 때마다 해당 과정을 반복하면 된다.
4. 보조 인덱스 (Secondary Indices)
보조 인덱스는 모든 검색 key값과 모든 레코드에 대한 포인터를 가지는 인덱스 엔트리로 된 밀집 인덱스여야 한다.보조 인덱스가 일부 검색 key값을 저장한다면 중간에 있는 검색 key값을 가진 레코드는 파일 어딘가에 있기는 하지만 전체 파일을 검색하지 않는 이상 찾을 수 없다.
일반적으로 보조 인덱스는 클러스터링 인덱스와 다른 구조를 가진다.
- 기본 인덱스(클러스터링 인덱스)의 검색 key : 후보 key가 아니지만 그 인덱스가 검색 key에 있는 값을 가지는 첫 번째 record를 가리키고 있다면 충분하다. 왜냐하면, 다른 레코드는 파일을 연속적으로 스캔하면서 가져올 수 있기 때문이다.
- 보조 인덱스의 검색 key : 이 값이 후보 key가 아니라면 각 검색 key값을 가지는 첫 번째 record를 가리키는 것으로 충분하지 않다. 똑같은 검색 key값을 가지는 나머지 레코드가 파일 내에 있지만 정확히 어디 있는지는 알 수 없기 때문이다. 왜 이렇게 되어 있냐면 레코드는 보조 인덱스의 검색 key값이 아니라 기본 인덱스의 검색 key값에 의해 순서가 정해져있기 때문이다.
그래서 보조 인덱스는 모든 레코드에 대한 포인터를 갖고 있어야 한다.
relation에 동일한 검색 key값을 가지는 record가 2개 이상 존재한다면 (즉, 2개 이상의 record가 인덱싱 속성에 대해 동일한 값을 가질 수 있다면) 이러한 검색 key를 비고유 검색 키(non-unique search key)라고 한다.
비고유 검색 키에 대해 보조 인덱스를 구현하는 방법은 다음과 같다.
기본 인덱스와는 다르게 보조 인덱스의 포인터는 레코드를 직접 가리켜서는 안된다. 대신에 보조 인덱스의 포인터는 그 파일에 대한 포인터를 저장하고 있는 버킷을 가리켜야 한다.
아래 그림은 instructor 파일에 대해 간접 참조를 사용하고 있는 보조 인덱스의 구조를 보여준다.

그러나 이 방법은 단점이 있다.
1) 간접 참조는 임의의 I/O 작업이 필요하기 때문에 인덱스에 접근할 때 시간이 오래 걸린다.
2) key에 중복이 거의 없거나 아예 없는 경우 전체 블록에 대한 버킷을 만들어야 하기 때문에 버킷에 공간을 할당하는데 많은 공간 낭비가 발생한다.
이번 장 뒷부분에서 이러한 단점을 피할 수 있는 효율적인 보조 인덱스 구현 방법을 살펴볼 예정이다.
클러스터링 인덱스에서 연속적으로 스캔하는건 효율적이다. 왜냐하면 파일에 있는 레코드가 인덱스의 순서와 동일한 순서로 물리적으로 저장되어 있기 때문이다.
하지만, 클러스터링 인덱스의 검색 key와 보조 인덱스의 검색 key 2개에 의한 순서로 파일을 물리적으로 저장할 수 없다.
왜냐하면, 보조 key 순서와 물리적인 key의 순서는 서로 다르기 때문이다.
그래서 만약에 파일을 보조 key 순서대로 스캔을 하려고 한다면 각각의 record를 읽는 것은 disk로부터 새로운 블록 읽기를 한 것과 같기 때문에 속도가 매우 느리다.
삭제와 삽입은 3번 절에서 설명한 내용을 보조 인덱스에 적용할 수 있다. 파일에 있는 모든 record에 대한 포인터를 저장하는 밀집 인덱스에 대해 앞서 설명한 방식과 유사하게 적용하면 된다.
보조 인덱스는 기본 인덱스의 검색 key가 아닌 다른 key를 사용하는 질의문의 성능을 향상시킨다. 그러나 이는 DB에 상당한 부담을 강요한다. 때문에 DB 설계자는 검색만을 위한 질의와 데이터 변경의 상대적인 빈도에 대한 평가에 기초해서 바람직한 보조 인덱스를 결정해야 한다.
5. 다중 key 인덱스
2개 이상의 속성으로 구성된 검색 key를 복합 검색 키(composite search key)라고 한다.
이 인덱스의 구조는 다른 인덱스 구조와 동일하고 차이점은 검색 key가 하나의 속성이 아닌 속성의 목록으로 되어 있다는 것이다.
목록은 튜플 형식으로 표현할 수 있다.
ex) 복합 검색 키(course_id, semester, year)를 가진 takes 릴레이션이 있다고 하자.
이러한 인덱스는 특정 학기/연도에 특정 교과 과정에 등록한 학생을 찾는데 유용하다. 복합 key에 대한 정렬 인덱스는 14.6.2에서 다룰 것이다.
'DB System Concepts 7th' 카테고리의 다른 글
| [DB] 14-3. B+ 트리 인덱스 파일 (0) | 2023.08.24 |
|---|---|
| [DB] Chapter 14. 인덱싱 & 14-1. 기본 개념 (0) | 2023.08.18 |
| [DB] 13-7. 메인 메모리 DB의 저장구조 (0) | 2023.08.18 |
| [DB] 13-6. Column-Oriented Storage (0) | 2023.08.06 |
| [DB] 13-5. Database Buffer (0) | 2023.08.05 |